미분적분학I 3.2 평균값 정리와 l'Hospital의 정리

안녕하십니까, 미래 메카트로닉스 제어공학자 controlling입니다.
이번에 다룰 내용은 굉장히 이론적인 정리와 굉장히 계산적인 정리 두 가지를 다루려고 합신다.

3.2 평균값 정리와 l'Hospital의 정리

우선, 굉장히 이론적인 평균값 정리를 증명하기 위하여 Rolle의 정리부터 알아보도록 하겠습니다.

정리 1. Rolle의 정리
함수 가 폐구간 에서 연속이고 개구간 에서 미분가능하며 이면 을 성립시키는 가 개구간  안에 존재한다.

증명)

사진을 확대해서 보시려면
사진을 클릭해주세요.

함수 가 폐구간 에서 연속이므로 최대/최소의 정리를 만족시킨다. 함수 가 에서 최댓값을 갖는다고 가정할 때 다음과 같은 부등식이 성립한다.

한편, 함수 는 개구간 에서 미분가능하므로 위 부등식에 의해 이다.
가 에서 최솟값을 갖는다고 해도 위와 같이 증명이 가능하다.

(위의 방식처럼 부등식을 세워서 미분가능성 따지면 증명이 가능합니다^^)

Rolle의 정리를 사용하여 평균값의 정리를 알아봅시다.

정리 2. 평균값의 정리
함수 가 폐구간 에서 연속이고 개구간 에서 미분가능하면 을 만족시키는 가 개구간  안에 존재한다.

증명)

사진을 확대해서 보시려면
사진을 클릭해주세요

두 점 과 를 지나는 직선을 나타내는 함수 가 존재한다고 하자. 함수 라고 가정할 때, Rolle의 정리에 의하여 을 만족시키는 값이 개구간  내에 반드시 존재한다. 이 때, 이므로, 이 성립한다.





이제는 상당히 계산적인 l'hospital의 정리를 반쪽짜리 증명을 하기 위해 Cauchy 정리를 알아보도록 합시다.

정리 3. Cauchy 정리
두 함수 와 가 폐구간 에서 연속이고 개구간 에서 미분 가능한 경우, 를 만족하는 가 개구간  안에 존재한다.

증명)

mean value theorem : 평균값 정리

codecogs로 LaTeX 한글 코딩이 안 되요 ㅠㅠ

이를 이용하여  l'hospital의 정리를 반만 증명할 겁니다. 우선, l'hospital의 정리가 무엇인지 먼저 말씀드리겠습니다.

정리 4. l'hospital의 정리
두 함수 와 가  근방에서 미분가능하고 이거나 인 경우, 이다.

저는 여기서 인 경우만 증명하겠습니다. 인 경우에 대한 증명은 다음 링크를 참고하세요.
https://ocw.dongguk.edu/contents/2011%5C20111220161258/pdf20111220161258.pdf
(사실 대부분 교양필수 미분적분학 듣는 사람들은 =0꼴만 증명하는 게 현실입니다만...)
(절대 내가 몰라서가 아니야! 아닙니다... 몰랐습니다...)

증명) 인 경우


예제) 서강대학교 2011년 편입학 기출문제

풀이)

답) 3

자, 또 이번 내용이 끝났습니다. 정리문제 풀면서 마치겠습니다.

아주대학교 2014년 편입학 기출문제

풀이)

답) 2

아주대학교 2013년 편입학 기출문제

풀이)

답) 4

건국대학교 2014년 편입학 기출문제

풀이) 우선, 함수 는 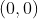을 지납니다.

따라서, 은 꼴이므로, 을 계산할 때 로피탈의 정리를 사용할 수 있습니다.

답) 2

경기대학교 2014년 편입학 기출문제

풀이) 경기대학교 배점 기준 난이도 下(2단계 중 1단계)

답) 1

경기대학교 2014년 편입학 기출문제

풀이) 경기대학교 배점 기준 난이도 上(2단계 중 2단계)

답) 2

하아... 바빠서요... 다음에 봐요!

참고문헌

청문각, <미분적분학>, 권희대 외 8명, pp. 46~49

서강대학교 2011년 편입학 기출문제

아주대학교 2014년 편입학 기출문제

경기대학교 2014년 편입학 기출문제