미분적분학I 1.5 ε과 δ, 수열의 수렴과 발산, 함수의 극한과 연속

안녕하십니까, controlling입니다.
제가 닉네임을 controlling이라고 했더니 우리 동명이가 저의 카테고리를 저의 닉네임으로 했더라고요. 음... 멋은 없네요 ㅋㅋㅋ
이제부터 블로그에 직접 치고 게시하기로 하였습니다. 수식도 html 안 쓰고 이미지 복사해서 붙이려고요. http://www.codecogs.com/latex/eqneditor.php codecogs 감사합니다 ㅠㅠ
오늘 진도 나가겠습니다.

1.5 ε과 δ, 수열의 수렴과 발산, 함수의 극한과 연속

 드디어 여기서 우리는 ε-δ 이론이라는 귀찮은데 알고보면 별 거 아닌 이론을 나가게 됩니다. 우선, ε로 수열의 수렴을 정의하도록 하겠습니다.

정의 1 수열의 수렴

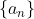
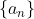
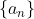
수열 가 존재한다고 가정하자. 자연수 에 대하여 인 모든 에 대하여  를 만족하는 어떠한 값에 대해서도  을 성립시키는 상수 이 존재한다고  할 때, 수열 는 로 수렴한다고 하고, 기호로 로 표기한다. 만약 위의 조건이 성립하지 않는다고 하면, 수열 는  발산한다고 한다.

이 정의로 수열의 수렴을 증명하기 위해서는 을 임의로 설정해야 합니다. 값을 설정하는 방법은 다음 예제를 풀면서 설명드리겠습니다. 값은 우리가 앞에서 구했던 방법으로 구하면 됩니다.

예제)
을 증명하시오.

풀이) 자연수 에 대하여 라고 가정할 때,  를 만족하는 어떠한 값에 대해서도  이 성립한다고 가정하면   이므로   이다. 따라서 이다.

응?) 을 가정해?
을 가정하는 법은 간단합니다. 부등식 의 관계를 꼴로 고칩니다. (위 예제에서는 )  이 때, 라고 가정하고 이 부등식을 에 대하여 정리합니다. (위 예제에서는    ) 정리하면 꼴로 나옵니다. 이 때, 로 설정하면 됩니다. (위 예제에서는 )

그럼 1.1에서 배운 명제 하나를 증명하겠습니다.

예제) 다음을 증명하시오.
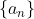
수열 , 이 각각 , 로 수렴할 때 다음이 성립한다.
임의의 실수 에 대하여 

풀이)  자연수 에 대하여 라고 가정할 때,  를 만족하는 어떠한 값에 대해서도    가 성립하므로, 양변에 를 곱하면 이므로 위 명제가 성립한다.

이렇게, 수열의 수렴과 관련된 증명은 위의 이론으로 모두 가능합니다.

그럼, 이제는 함수의 극한의 정의에 대하여 이야기하겠습니다.

정의 2. 함수의 극한
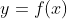
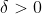
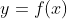
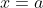
함수 가 존재한다고 하였을 때, 어떠한 에 대해서도 다음과 같은 조건을 만족하는 이 있다면 함수 는 에서 극한값 을 갖는다고 한다.

•  일 때  

위를 기호로 나타내면 라고 한다.

이를 이용하여 함수의 연속을 정의하면 다음과 같습니다.

정의 3. 함수의 연속
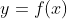
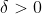
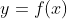
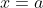
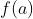
함수 가 존재한다고 하였을 때, 어떠한 에 대해서도 다음과 같은 조건을 만족하는 이 있다면 함수 는 에서 극한값 을 갖는다고 한다.

• 일 때

이는 를 서술한 것과 같습니다.
이를 이용하여 1.4에서 배운 명제 하나를 증명하겠습니다.

예제) 다음을 증명하시오.
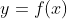
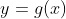
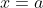
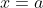
함수 와 가 에서 연속이면 도 에서 연속이다.

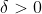
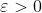
풀이) 이라고 가정할 때 어떠한 에 대해서도 이 성립한다고 할 때 과 를 만족시키는 이 존재한다. 따라서, 다음과 같은 수식이 성립한다.

따라서, 위 명제가 성립한다.
위 이론으로 함수의 연속과 관련된 정리를 증명할 수 있습니다.

이번 이론은 문제를 푸는 것 보다는 그동안 배워왔던 수열의 수렴과 관련된 정리와 함수의 연속과 관련된 정의를 직접 증명해 보는 것이 좋을 것 같슶니다. (문제도 별로 없어요...) 다음에 봐요! 안녕!