2월도 이제 중순이고, 저는 곧 개학이며, 학부연구원이 기다리고 있습니다.
설레네요. 저는 상당히 바빠질 예정입니다만... 여러분은 지금까지 무엇을 하셨습니까...?!
저보다는 보람있게 보냈기를...
오늘 나갈 내용은 다음과 같습니다.
2.2 여러가지 미분법
이번에 배울 것은 여분과 관련된 여러가지 연산을 배울 것입니다. 우선, 도함수와 관련된 기본공식을 정리하도록 해보겠습니다.
정리 1. 도함수의 기본공식
함수
(1)
(2)
(3)
위 공식에 대한 증명은 도함수의 정의인
정리 1.(4) 증명
여기서 중요한 미분공식 중 하나를 다룰 것입니다. 다음 공식입니다.
정리 2. 도함수 공식 : 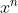
증명)
정리 3. 도함수 공식 :
증명)
그리고, 증명하지 않고 넘어가겠지만, 상수를 미분하면 0입니다. 구지 증명하고 싶으시다면 미분의 정의를 이용하여 증명하시면 됩니다. 상수함수는 변화가 없으니 분모에 0이 나오는, 차마 어이가 없어 내가 왜 이걸 증명하려 했지?라는 소리가 나올 것입니다!
자, 여기서 다음 내용 나가기 전에 중요한 것 하나! 표기법 하나 짚고 넘어가겠습니다. 함수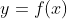 를
를  에 대하여 미분한 것을
에 대하여 미분한 것을 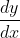 라고도 표현합니다. 또한,
라고도 표현합니다. 또한, 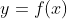 를
를  에 대하여
에 대하여  번 미분한 것을
번 미분한 것을  라고 표현합니다. 다음 배울 내용은 합성함수의 미분법입니다.
라고 표현합니다. 다음 배울 내용은 합성함수의 미분법입니다.
정리 4. 합성함수의 미분법(연쇄법칙:chain rule)
함수  가 존재한다고 가정하였을 때,
가 존재한다고 가정하였을 때,  이고, 이는
이고, 이는  를 성립시킨다.
를 성립시킨다.
증명)
이제 다룰 미분법은 음함수의 미분법입니다.  꼴의 함수가 있다고 할 때,
꼴의 함수가 있다고 할 때,  는
는  에 대하여 음함수라고 합니다. 이 때,
에 대하여 음함수라고 합니다. 이 때,  와
와  의 관계식에서 양변을
의 관계식에서 양변을  에 대하여 미분하여
에 대하여 미분하여  에 대하여 정리하는 방법을 음함수의 미분법이라고 합니다. 예시를 들어보겠습니다.
에 대하여 정리하는 방법을 음함수의 미분법이라고 합니다. 예시를 들어보겠습니다.
예제) 으로부터
으로부터 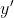 를 구하시오
를 구하시오
풀이)
예제)
음함수의 미분법을 이용하여 방금 배운 미분 공식을 확장하여봅시다.
정리 5. 도함수 공식 :
증명)
오늘은 이론이 살짝 많네요. 이번에는 역함수의 미분법을 알아보도록 하겠습니다.
정리 6. 역함수의 미분법
증명) 함수
* 한편, 합성함수의 미분을 사용하여 다음과 같은 표현도 가능합니다.
예제) 인하대학교 2014년 편입학 기출문제
답)d
한편, 매개변수 방정식으로 나타낸 두 변수 사이의 도함수 관계도 구할 수 있습니다.
정리 7. 매개변수 방정식의 미분법
그럼 정리문제를 풀면서 이번 순서 마치도록 하겠습니다.
연세대학교 서울캠퍼스 2011년 공업수학(1) 1차 기출문제
풀이) 오른쪽 그림처럼 좌표
따라서,
따라서,
답) 5
아주대학교 2014년 편입학 기출문제
풀이) 음함수의 미분법
답) 3
풀이) 음함수의 미분법
답) 3
아주대학교 2012년 편입학 기출문제풀이) 음함수의 미분법
답) 2
아주대학교 2011년 편입학 기출문제풀이) 음함수의 미분법
우선, 함수
따라서,
답) 3
하... 오늘도 문제 찾느라 힘들었는데요... 다음 단원부터는 그런 고통, 안 겪어도 될 거 같습니다. 드디어 초월함수의 미분이 나오거든요! 다음에 봅시다!
참고문헌
청문각, <미분적분학>, 권희대 외 8명, pp. 29~34
아주대학교 2011, 2012, 2013, 2014년 편입학 기출문제
인하대학교 2014년 편입학 기출문제
연세대학교 서울캠퍼스 2011년 공업수학(1) 1차 기출문제








댓글 없음 :
댓글 쓰기