미분적분학I 1.2 함수

안녕하십니까, 미래 메카트로닉스 제어공학자 controling입니다.
몇 장 안 되는 내용을 치는 데에도 시간이 많이 걸리네요... 블로그 포스팅 하시는 여러분 존경합니다 ㅠㅠ
원래는 LaTeX 코딩을 도와주는 codecogs사의 codecogs 블로그 설치를 이용하여 작성했는데, 호환이 안 되는 부분도 있고, 제가 LaTeX를 잘 몰라서 코딩하는 것도 쉽지 않은 거 같아 그냥 codecogs의 홈페이지에서 변환한 것을 이미지로 옮겨서 붙여넣는게 속 편한 거 같습니다.

이번 내용 나가겠습니다.

1.2 함수

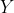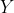오늘부터 함수에 대하여 공부하도록 하겠습니다. 함수에 대하여 공부하려면 함수가 무엇인지 알아야죠. 함수란 무엇입니까? 함수란, 두 집합 와 가 존재한다고 하였을 때, 집합 의 원소 하나가 집합 의 원소 하나에 대응되는 것을 이야기합니다.  예를 그림과 함께 나타내겠습니다.

[그림1] 두 집합이 함수 관계를 이루고 있다.

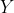
왼쪽의 [그림1]은 집합 의 한 원소가 집합 의 하나의 원소에 대응되는 관계로, 두 집합은 함수관계에 있다고 할 수 있습니다.

[그림 2] 두 집합이 함수 관계를 이루고 있지 않다.

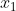
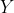
 [그림 2]는 집합 의 한 원소 가 집합 의 하나 이상의 원소에 대응되는 관계로, 두  집합은 함수관계에 있지 않습니다.













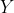
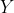
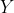
집합 와 집합 가 서로 함수 관계를 이룰 때, 이를 간단히 기호로 로 나타냅니다. 물론, 여기서 는 다른 것이 와도 좋습니다. 함수명 이외의 의미는 없기 때문이죠.  여기서 집합 는 함수 의 정의역이라고 하고,  집합 는 함수 의 공역이라고 합니다. 집합 의 임의의 원소 가 존재한다고 할 때,  는  함수 에 대한 의 함숫값이라고 합니다.  함숫값은 에 대응되는 집합 의 원소의 값입니다. 치역은 정의역의 원소로 얻어낸 함숫값들의 집합인데요, 기호로는 로 표시할 수 있습니다.

[그림 3] 일대일대응이 아닌 함수

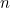
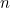
함수 하면 중학생때 죽어라 들었던 것이 일대일대응과 역함수인데요, 우선 일대일 대응부터 이야기하겠습니다. 함수의 정의과 일대일대응을 헷갈리시는 분들이 계시는 거 같아요. 일대일대응은 정의역의 원소와 공역(치역이라고 해도 명제가 성립합니다.)의 원소가 1:1로 대응되는 것입니다. 함수는 정의역의 원소와 공역(혹은 치역)의 원소가 1:(단, 은 자연수)으로 대응되면 됩니다. 예를 들어, [그림 1]의 두 집합은 함수 관계를 이루면서 일대일 대응입니다.  하지만, [그림 3]의 두 집합은 일대일대응이 아닙니다. 다만 함수는 맞죠. 집합 의 원소들은 모두 집합 의 하나의 원소와 짝지어지기 때문에 함수의 정의에 위배되지 않습니다.
함수 관계가 성립하는 두 집합에 대하여 일대일대응 관계가 성립한다고 할 때, 이 함수는 일대일함수, 또는 단사함수라고 일컫습니다. 한편, 치역과 공역이 일치하는 함수는 전사함수라고 일컫습니다. 갑자기 황당하게 전사함수를 언급한 이유는 전단사함수를 소개하기 위해서입니다. 전단사함수는 전사함수이면서 단사함수인 함수를 일컫습니다.

이제, 역함수에 대하여 설명하겠습니다. 우선, 이 사실을 주지할까 합니다.
"역함수도 함수다."
함수 가 일대일함수라고 할 때, 함수 와 가 존재한다고 했을 때, 함수 는 함수 의 역함수입니다.  함수 를 일대일 함수라고 가정한 이유는 함수 의 역함수도 함수이기 때문입니다. 예를 들어봅시다, 만약 함수 가 일대일함수가 아니라고 가정할 때, 는 함수가 되지 못할 것입니다. 집합 의 원소 중에 집합 의 두 개 이상의  원소가 대응되는 원소가 분명히 존재하기 때문이죠. 예를 들어, [그림 3]의 화살표를 반대방향으로 하면 에 대응되는 집합 의 원소가 2개이므로 함수의 정의에 위반됩니다. 따라서, [그림 3]의 함수는 역함수가 없습니다. 또한, 일대일함수의 역함수 역시 일대일함수입니다.
어떤 함수의 역함수는 그 함수명에 를 붙입니다. 예를 들어, 함수 의 역함수는 로 표시합니다.
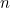
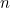
그리고, 어떤 함수에 번 역함수를 취한 함수는 그 함수에 를 붙입니다. 예를 들어, 함수 에 번 역함수를 취한 함수는 로 표시합니다. 아마 이 내용은 미적분학엔 안 나올겁니다. 선형대수에서는 잘 쓰이는 표현입니다. 혹시 이 내용을 학교에서 배우지 않았다면 학교 시험에 함부로 쓰지 마세요...

역함수의 성질에 대하여 이야기드리겠습니다.
1. 어떤 함수의 역함수의 정의역은 어떤 함수의 치역이다.(의 정의역은 의 치역)
2. 어떤 함수의 역함수의 치역은 어떤 함수의 치역이다.(의 치역은 의 정의역)
3. 어떤 함수의 역함수를 홀수번 취한 함수는 어떤 함수의 역함수이다. ()
4. 어떤 함수의 역함수를 짝수번 취한 함수는 어떤 함수의 자신이다. ()

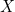
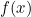
이제 합성함수에 대하여 알아봅시다. 세 집합  사이에 ,와 같은 함수 관계가 성립한다고 했을 때,  집합 에 속하는 임의의 원소   를 가정하면 입니다. 이 때, 는 함수 의 정의역의 원소가 됩니다. 따라서, 와 같은 표현이 가능합니다. 이러한 함수를 와 의 합성함수라고 하며,  와 같이 나타냅니다.
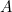
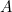
특수한 케이스를 설명하기 위해 특이한 함수를 설명하려 합니다. 라는 함수가 있습니다. 이 함수는 집합 의 함수의 각 원소를 자기 자신으로 대응시키는 함수를 뜻합니다. 이를 집합 에 대한 항등함수라고 합니다. 만약에 두 집합 에 대하여 , 과 같은 함수 관계가 성립한다면 두 함수 사이에는 역함수 관계가 성립하며, 라고 할 수 있습니다.

보통 우리는 함수를 꼴로 씁니다. 여기서 를 독립변수, 를 종속변수라고 합니다.  는 어떠한 변수의 영향도 받지 않고 값을 변화시킬 수 있지만, 의 값은 의 영향을 받기 때문에 그렇게 부릅니다.

우리는 고등학생때 구간의 표기법을 배웠습니다. 까먹었을수도 있기에 다시 정리해보겠습니다.






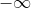
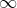
위의 범위 표기에서 가 인 경우 왼쪽 괄호는 반드시 소괄호로 표기하셔야 합니다. 마찬가지로, 가 인 경우 오른쪽 괄호는 반드시 소괄호로 표기하셔야 합니다. 한편, 양쪽 괄호가 모두 대괄호인 경우의 구간을 폐구간, 양쪽 괄호가 모두 소괄호인 경우의 구간을 개구간이라고 합니다.

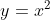
예제)  의 정의역과 치역을 구하시오

(답)  정의역 :  , 치역 :  

 

 

[그림 4] 우함수 그래프(가로축 : x, 세로축 : y)

[그림 5] 기함수 그래프(가로축 : x, 세로축 : y)

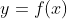
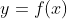
함수는 그 함수의 독립변수와 종속변수의 좌표로 그 그래프를 구할 수 있습니다. (독립변수가 2개 이하인 경우에만 가능합니다. 당신이 3차원에 살고 계시다면 독립변수가 3개인 함수의 그래프는 절대 못 그립니다.) 함수의 그래프란 함수의 좌표들을 좌표평면(좌표공간, 혹은 수직선)에 표시한 것이기 때문이죠. 말은 되게 어렵지만, 함수의 그래프 하면 떠오르는 것이 있을 것입니다. 바로 그것입니다. 그런데, 어떤 함수는 좌표축이나 원점에 대하여 대칭인 함수가 있습니다. 그것을 우리는 우함수와 기함수라고 합니다. 라는 함수가 있다고 가정하면 우함수는 함수 의 그래프가 축에 대칭인 함수이며, 기함수는 그래프가 원점에 대칭인 함수입니다. 축에 대칭인 함수는요? 아이쿠,  꼴의 함수는  축에 대칭일 수가 없습니다. 하나의 값에 두 개 이상의 값이 대응되거든요. [그림 6]을 보시면 무슨 말일지 알 수 있을겁니다.
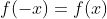
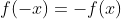
우함수는 수식으로 표현하면 입니다. 기함수는 수식으로 표현하면 입니다. 기함수와 우함수는 나중에 미적분 할 때 계산과정을 그나마 줄여주기 위해 사용합니다. 그렇다고 미적분 계산이 유쾌해지는 것은 아닙니다. 

[그림 6] x축에 대칭인 함수

다음으로 알아볼 내용은 함수의 연산인데요, 중요한 것은 아니니 정의만 간단하게 보겠습니다.
 (는 상수)



마지막으로, 여러가지 함수에 대하여 알아보겠습니다.
1. 다항함수 모든 항이 종속변수의 음이 아닌 정수차항으로 이루어진 함수를 이야기합니다.
 꼴을 보입니다.
2. 지수함수 양수의 종속변수 제곱꼴의 함수입니다.
 꼴입니다.
3. 로그함수 로그가 들어간 함수입니다.(...)
 꼴입니다.
4. 삼각함수 가 들어간 함수를 말합니다.
삼각함수에 대해서 여러분이 알아야하실 것이 있습니다. 삼각함수 공식인데요, 공대생이라면 미분적분학 과목을 이수하신 분이라면 증명이고 자시고 그냥 외우면 됩니다. 하지만, 제가 지금 포스팅하는 것이 수학이기 때문에 각각에 대한 증명을 올리고자 합니다.

[그림 7]

합차 공식
(1)  
증명) [그림 7]을 참고하면


   

 에 를 대입하면 차 공식도 증명됩니다.

(2)
증명) [그림 7]과 (1)의 증명과정에서 얻은 정보를 이용하면





 에 를 대입하면 차 공식도 증명됩니다.

(3)
     
증명)

 에 를 대입하면 차 공식도 증명됩니다.

배각 공식
(1)
증명)
                      
                      

(2)
증명)
                       
                      
                      
                     
                     
                     

삼배각 공식
(1) 
증명)
                       
                      
                      
                      
                      

(2)
증명)
                       
                      
                      
                       
                      
                       

반각공식
 (1)
      
(2)
    
반각공식의 두 공식은 배각공식 (2)의 에  를 대입하여 정리하시면 증명하실 수 있습니다.

이번 단원에서 다룰 내용은 끝났습니다. 후... 왜 오늘 내용은 길어보이죠... 기분 탓인가... 정리 문제 풀어보겠습니다^^

2014년 광운대학교 편입 기출 17번

풀이) 광운대 기준 난이도 중짜리 문제입니다.

답) 2

2014년 광운대학교 편입 기출 18번

풀이) 광운대 기준 난이도 중짜리 문제입니다.
사실 눈치가 있다면 푸는 방법을 몰라도 답을 알 겁니다.
그래도 정석대로 갑시다
첫 번째 식 $f(g(x)) = f(x)$으로부터 $f(g(g(x)))=f(x)$임을 알 수 있습니다. 이건 문제를 많이 풀어보셔야 빨리 보일 수 있는 거 같아요. 문제를 봤을 때, $f(25)$가 왠지 $f(-5)$에 대한 식으로 정리되어야 할 거 같다는 느낌을 받으셨으면 좋겠습니다. 25는 -5의 제곱이죠. $g(g(x))=x^2$에 의해 $g(g(-5))=25$입니다. 그럼 아까 알아냈던 $f(g(g(x)))=f(x)$를 이용하여 문제를 풉시다. $f(25)=f(g(g(-5)))=f(-5)$입니다. 따라서, $f(25)-f(-5)=0$입니다.

답) 3

 

2014년 광운대학교 편입 기출 21번

풀이) 광운대 기준 난이도 하짜리 문제입니다.

증가함수+증가함수=증가함수이죠. 는 증가함수 두 개와 상수를 더한 함수입니다. 따라서 증가함수입니다.

는 가 양수가 아닌 경우 증가함수가 아닙니다. 증가함수에 0을 곱하면면 그 함수의 값은 0이며 증가함수에 음수를 곱하면 그 함수는 감소함수입니다.

은 가 음수인 경우 증가함수가 아닐 수 있습니다. 예를 들어, 이라고 하면 입니다.

답) 1

 

하... 몇 문제 더 넣고 싶었지만 피곤해서 자려고요... 다음 단원에서 봐요!

 

참고문헌

청문각 <미분적분학> 권희대 외 8명 著 pp. 3~6

광운대학교 2014년 편입 기출문제